In this unit we have been talking about identity, which is the proof we show in order to understand or solve a problem. The Pythagorean Theorem is another way to prove a problem (a^2+b^2=c^2). In order to prove our answer right, we have to cancel it with the answer, if it is equaled to 1 or r^2, then it has to be canceled by 1 or r^2. Another example, will determine that we use the ratios of the Unit Circle. The ratio of cosine and sine is the same thing as the Pythagorean Theorem, it is just moved around.
2. Show and explain how to derive the two remaining Pythagorean Identites from sin^2x+cos^2x=1. Be sure to show step by step.
a) Deriving Secant and Tangent [sin^2x+cos^2x=1] we will have to divide it by dividing it to cos^2x to get the inverse function od cosine, Sec.
b) you can simplifies it once more to get tan^2+1=sec^2X. (Tan^2x= sin^2x/cos^2x)
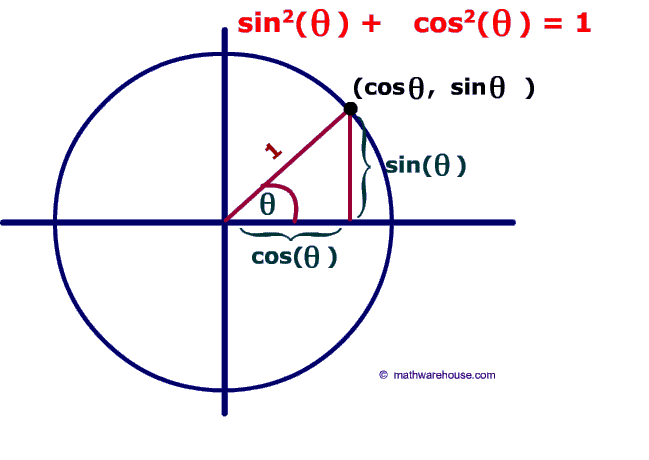
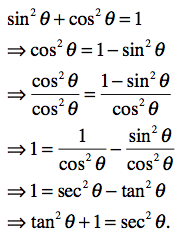
No comments:
Post a Comment