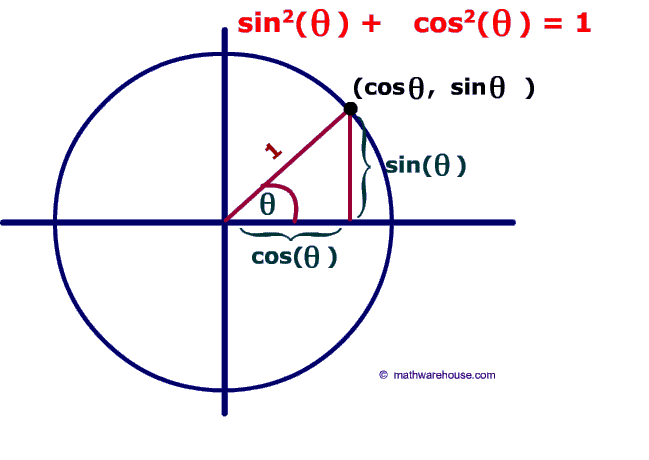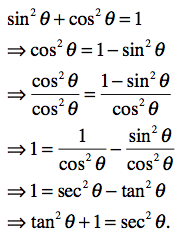SP#7 Unit Q: Concept 2

Visit her awesome blog here!

This student problem was made in a collaboration with Danielle O.

WPP#10 Unit P: Concepts 13-14

The first solution, is when we have to figure out how far they are from the restaurant.

ID#3: Unit Q: Concept 1. Pythagorean Identites.

1. Where does where sin^2+cos^2x=1 come from to begin with? You should be referring to Unit Circle ratios and the Pythagorean Theorem in your expectation.
In this unit we have been talking about identity, which is the proof we show in order to understand or solve a problem. The Pythagorean Theorem is another way to prove a problem (a^2+b^2=c^2). In order to prove our answer right, we have to cancel it with the answer, if it is equaled to 1 or r^2, then it has to be canceled by 1 or r^2. Another example, will determine that we use the ratios of the Unit Circle. The ratio of cosine and sine is the same thing as the Pythagorean Theorem, it is just moved around.

 2. Show and explain how to derive the two remaining Pythagorean Identites from sin^2x+cos^2x=1. Be sure to show step by step.
a) Deriving Secant and Tangent [sin^2x+cos^2x=1] we will have to divide it by dividing it to cos^2x to get the inverse function od cosine, Sec.
b) you can simplifies it once more to get tan^2+1=sec^2X. (Tan^2x= sin^2x/cos^2x)

BQ#1: Unit P Concept 4 : Area of an Oblique Traingle.

1. Law of Sines - Why do we need it? How is derived from what we already know?
The law of Sines is used for non-right triangles. For example, trig function is used for right triangles only.  We need the law sine in  order to find a side while we know the opposite angle. Triangles like AAS OR ASA, need to determine all three angles and sides.
It is derived by drawing a perpendicular line across from angle B. This will be called height. Once we have a height, we can solve any angle by using SOH CAH TOA. You equal the equation of the angle with the equation of the opposite side, and solve.

4. Area Formulas - How is the "area of an oblique" triangles derived? How does it relate to the area formula that you are familiar with.
The area of an oblique triangle is derived by having two side and one angle. The height is unknown, so we use the formula 1/2b(csinA). This equation is one out of the three that can be used, since we have three sides and angles. It all depends what they give you to start with. All students are familiar with A= 1/2bh to find the area of a triangle. This formula was used since they would give us the height. Now we do not get the height, so we substitute it with a side(sine of and angle).

WPP#12 Unit O Concept: 10: Solving Of Elevation and Depression Word Problems (able to define the longitute of a slant angle)

Saving Gwen Stacy

Gwen Stacy is captured my the evil Lizard. The lizard has Gwen Stacy on top of a building, where Spiderman cant reach. We have to help Spiderman find the length of each building to get to Gwen Stacy.

 

Spiderman starts on the first building,he has a little bit of web. This means he needs an exact height of the first building. The degree for the first triangle is 56 degrees, and the adjacent is 18 inches. Solve for the height, which is "x".

After he get to the second building, and has no choice but to jump off. This creates another height to figure out. The hypotenuse is 26 inches, and the degree is 32 degrees. Solve for "x".

In order to solve these triangles, we get to use SOH CAH TOA. Since the first triangle gives us the adjacent and "x" for opposite, we get to use Tangent. Tangent of 56=x/18. X will equal 26.69 inches.

Second Triangle has given us the Hypotenuse, 26inches, and the opposite is "x". In this triangle, we will be using Sine(SOH). sine of 32=x/26. This should equal 22.048 inches.

 

I/D#2 Unit O Concept 7-8: How can we derive special right triangles?

 

 

 

Looking at his triangle, we see that is two 30-60-90 degree triangles. We had to divide this equilateral triangle. It has all three same sides, and three same angles. The hypotenuse is equaled to one, and one side is 1/2. Using the Pythagorean theorem, we will solve for "b". C should be rad3.

 

The pattern of this 30-60-90 triangle can be defined with any number, You start off by choosing a number, and plug it in for "n". You get 1n for a, and 2n for the hypotenuse. You will times two to rad3/2.

 

To get a 45-45-90 degree triangle by cutting a perfect square, slanted. This will divide two angle which equal 90 degrees. Both sides are 1, then you solve for the hypotenuse. C should be rad2.

 

As like the other triangle, any number can be used since it only gets the square bigger or smaller. Either way. the sides will be the same number. Since the sides can change number, we have to add "n" on each side in order to solve.

 

Reflections:

 

1. Something I never noticed about special right triangles is the fact that is related to the unit circle.

2. Being able to derive these patterns myself aids my learning by explaining the reasons we get specific answers to the problems given in this concept.