Unit V; BQ#7

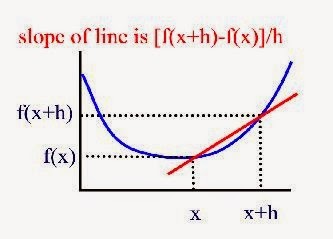
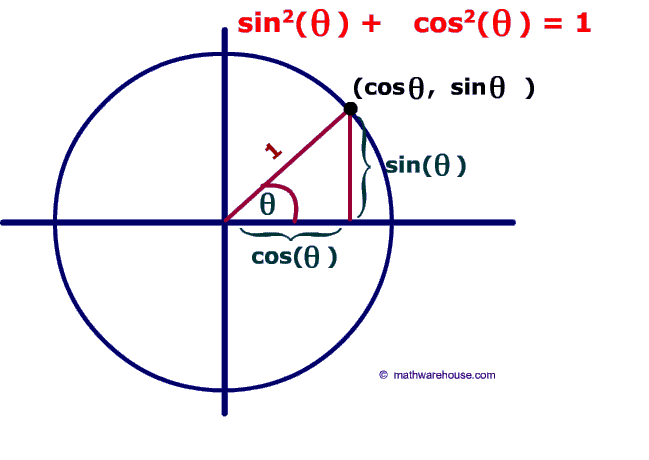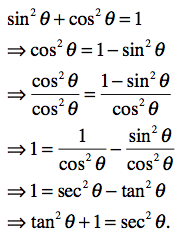Q. Explain in detail where the formula for the difference quotient comes.

A. The difference quotient is related to the slope formula y2-y1/x2-x1. This means the difference quotient is a fancy way to find the slope of a graph. Also the problem that they give us to use the difference quotient, is just a formula of y=mx+b. we substitute the y-axis with the formula of f(x). This will give us f(x^2)-f(x)/x2-x1. The h is the horizontal direction you will have to go in order to get to the other point.

Unit U BQ#6

Big Questions:
Q.What is continuity? What is discontinuity?
A. Continuity, is when the graph is predictable, it can go in any direction, it has no holes, jump or brakes, and you can draw it without picking up the pencil. Discontinuity is when the limit does not exist this usually occurs when there is a vertical asymptote.

Q. What is limit? When does limit exist? When does t not exist? What is the difference?
A. A limit is the intended height of the function. The limit exist when there is a removable discontinuity, a jump discontinuity. The limit does not exist when it occurs to non-removable discontinuity. The height of a function and the value is the actual height.

Q. How do we evaluate limits numerically, graphically, and algebraically?
A. Numerically- we create a chart in order to find the certain points of the limit or value.
     Graphically- Evaluate each graph with the name of discontinuity value.
     Algebraically- by plugging  in the x value, and figure out if it is indeterminate

BQ#4 Unit T

Big Question
Q. Why is a "normal"  tangent graph up hill, but a "normal" cotangent downhill?

A. Since cotangent is the inverse of tangent, the asymptotes will sift in different directions. Which will create different rotations and have different beginning points.

BQ#3 Unit T

Big Question
 
Q. How do the graphs of sine and cosine relate to each other?

A. Sine and cosine both have the denominator as zero, which makes them equal to one. They are inverse to their asymptotes, and makes slanted lines. The waves will always equal to zero, since the radius is the denominator.

BQ#5 Unit T: Concept 3

Big Question

Q. Why do sine and cosine NOT have asymptotes, but the other four trig graphs do? Use circle ratios to explain.

A. Asymptotes are considered undefined. Sine and cosine do not have asymptotes because the functions have a zero and will always have a denominator of one, and repeats forever.

BQ#2 Unit T

Big Questions:
 Q. How do the trig fractions relate to the Unit Circle?
A. If we focus on Sine, we know that sine is positive and negative on certain sides. The Unit circle is the same by expanding to a graph line, and not a circle. The periods will be the one time point that will go through the cycle. The amplitudes is the distance between the highest and lowest points on the graph. It is like the angle of a point in a unit circle.

Reflection #1 Unit Q

Questions

1. When you verify a trig function, it means you will have to solve the function until you get the same answer as the other side. You cannot touch the other side, that is your answer and cannot be changed
2. One of the tips is memorizing the ratio, rational identities. It helps a lot getting and you do not waste time while working on the test or problems. Also finding out what they have in common until I actually work on them.
3. Verifying trig function had one similar thing, and that is not touching the other side of the equal side. The on thing I would do is changing them to fractions and also change to the same trig functions. They always have something in common.

SP#7 Unit Q: Concept 2

Visit her awesome blog here!

This student problem was made in a collaboration with Danielle O.

WPP#10 Unit P: Concepts 13-14

The first solution, is when we have to figure out how far they are from the restaurant.

ID#3: Unit Q: Concept 1. Pythagorean Identites.

1. Where does where sin^2+cos^2x=1 come from to begin with? You should be referring to Unit Circle ratios and the Pythagorean Theorem in your expectation.
In this unit we have been talking about identity, which is the proof we show in order to understand or solve a problem. The Pythagorean Theorem is another way to prove a problem (a^2+b^2=c^2). In order to prove our answer right, we have to cancel it with the answer, if it is equaled to 1 or r^2, then it has to be canceled by 1 or r^2. Another example, will determine that we use the ratios of the Unit Circle. The ratio of cosine and sine is the same thing as the Pythagorean Theorem, it is just moved around.

 2. Show and explain how to derive the two remaining Pythagorean Identites from sin^2x+cos^2x=1. Be sure to show step by step.
a) Deriving Secant and Tangent [sin^2x+cos^2x=1] we will have to divide it by dividing it to cos^2x to get the inverse function od cosine, Sec.
b) you can simplifies it once more to get tan^2+1=sec^2X. (Tan^2x= sin^2x/cos^2x)

BQ#1: Unit P Concept 4 : Area of an Oblique Traingle.

1. Law of Sines - Why do we need it? How is derived from what we already know?
The law of Sines is used for non-right triangles. For example, trig function is used for right triangles only.  We need the law sine in  order to find a side while we know the opposite angle. Triangles like AAS OR ASA, need to determine all three angles and sides.
It is derived by drawing a perpendicular line across from angle B. This will be called height. Once we have a height, we can solve any angle by using SOH CAH TOA. You equal the equation of the angle with the equation of the opposite side, and solve.

4. Area Formulas - How is the "area of an oblique" triangles derived? How does it relate to the area formula that you are familiar with.
The area of an oblique triangle is derived by having two side and one angle. The height is unknown, so we use the formula 1/2b(csinA). This equation is one out of the three that can be used, since we have three sides and angles. It all depends what they give you to start with. All students are familiar with A= 1/2bh to find the area of a triangle. This formula was used since they would give us the height. Now we do not get the height, so we substitute it with a side(sine of and angle).

WPP#12 Unit O Concept: 10: Solving Of Elevation and Depression Word Problems (able to define the longitute of a slant angle)

Saving Gwen Stacy

Gwen Stacy is captured my the evil Lizard. The lizard has Gwen Stacy on top of a building, where Spiderman cant reach. We have to help Spiderman find the length of each building to get to Gwen Stacy.

 

Spiderman starts on the first building,he has a little bit of web. This means he needs an exact height of the first building. The degree for the first triangle is 56 degrees, and the adjacent is 18 inches. Solve for the height, which is "x".

After he get to the second building, and has no choice but to jump off. This creates another height to figure out. The hypotenuse is 26 inches, and the degree is 32 degrees. Solve for "x".

In order to solve these triangles, we get to use SOH CAH TOA. Since the first triangle gives us the adjacent and "x" for opposite, we get to use Tangent. Tangent of 56=x/18. X will equal 26.69 inches.

Second Triangle has given us the Hypotenuse, 26inches, and the opposite is "x". In this triangle, we will be using Sine(SOH). sine of 32=x/26. This should equal 22.048 inches.

 

I/D#2 Unit O Concept 7-8: How can we derive special right triangles?

 

 

 

Looking at his triangle, we see that is two 30-60-90 degree triangles. We had to divide this equilateral triangle. It has all three same sides, and three same angles. The hypotenuse is equaled to one, and one side is 1/2. Using the Pythagorean theorem, we will solve for "b". C should be rad3.

 

The pattern of this 30-60-90 triangle can be defined with any number, You start off by choosing a number, and plug it in for "n". You get 1n for a, and 2n for the hypotenuse. You will times two to rad3/2.

 

To get a 45-45-90 degree triangle by cutting a perfect square, slanted. This will divide two angle which equal 90 degrees. Both sides are 1, then you solve for the hypotenuse. C should be rad2.

 

As like the other triangle, any number can be used since it only gets the square bigger or smaller. Either way. the sides will be the same number. Since the sides can change number, we have to add "n" on each side in order to solve.

 

Reflections:

 

1. Something I never noticed about special right triangles is the fact that is related to the unit circle.

2. Being able to derive these patterns myself aids my learning by explaining the reasons we get specific answers to the problems given in this concept.



I/D#1: Unit N Concept 7-9: knowing all degrees and radians

 

Before starting Concept 7-9 in Unit N, we worked on an activity that derives the Unit Circle. This means we got extra help for us to understand the Unit Circle. This activity will help us understand how to get the radians on the unit circle. This activity contained three triangles, and we had to label and draw coordinates.

First step: Label according to the rules of Special Right Triangles: You could have just googled  "rules of Special Right Triangles" and would have gotten the hypotenuse is 2x, and one leg is x, the other leg is x radical 3.
Second Step: Simplify the three sides of the triangle fairly in a way such that hypotenuse equals 1: This meant that the hypotenuse has to equal one. In order to get 2x to equal one, is dividing it by 2x. This meant to divide everything in 2x, since it said simplify fairly. Hypotenuse=1, leg1= 1/2, and leg2=radical 3/2.
Third step: Label the hypotenuse "r": The hypotenuse is labeled "r"
Fourth Step: Label the horizontal value "x": Leg 2 is labeled "x"
Fifth Step: Label the vertical value "y": Leg1 is labeled "y"
Sixth step: Draw a coordinate plane for each triangle, with the origin being located at the labeled angle measured: You will have to draw a graph by the triangle, so the triangle will be on Quadrant 1.
Seventh Step: label all three vertices of each triangle as ordered pairs: Each corner of the triangle is a vertices, and has to be plotted. Also Labeled.

1. The 30 degree triangle is labeled and simplified, as the instruction has been explained. After you found the vertices, you will be able to find the radiant and vertices. This will always have a radical 3.
2. The 45 degree triangle is different than the 30 degree triangle. This will always have radical 2/2, or radical 2.
3. The 60 degree triangle is similar to the 30 degree triangle. This will have a radical 3, radical 3/3.

4. This activity helped me find my vertices of my unit circle, by using the special rights of triangle, and having the hypotenuse equal to 1. It also helped my find the radians of the unit circle. Before I will have not choice to just memorize the unit circle without knowing how to solve for them. This activity answered my question. If I forget the radian, now I know hoe to solve it.
5. If we place this triangle on a different quadrant, the signs will change. This is based on ASTC. When it lies on the first then all numbers will be positive. If it lies on Second then sine and cosecant will be positive, and the rest will be negative. Third quadrant, tangent and cotangent will be positive and the rest will be negative. Fourth quadrant, cosine, and secant will be positive and the rest will be negative.

1. The coolest thing I learned on this activity was finding out where did we get the different radians and vertices for the Unit Circle.
2. This activity will help me a lot by giving me a a second option on how to find the radian or degrees in my unit circle. In case I forget when I am trying to fill out by memory.
3. something I never realized before about special right triangle and the unit circle is that they are both derive information to me in order to find answers for concept 8 and 9.

RWA#1: Unit M Concept 5 : Graphing Ellipses given equation.

1. Mathematical Equation:

• A curved line creating a close loop, where the total of the distance from the foci. The foci, creates the sum of the constant.
• A set of all points such that the sum of the distance from two points is a constant.

2. Description:

• Algebraically: (x-h)^2/a^2+(y-k)^2/b^2=1
• Graphically:
  
• key features: Standard Form- is the algebraically way to solve the ellipse.

Center: The center point will determine where the ellipse will be placed

                       2 vertices: These points are that will connect with center, and show what kind of ellipse it is

 

                       Major Axis: Depending on the minor, it will determine if it is skinny or fat.

                       Minor Axis: Depending on the major, it will determine if it is skinny or fat.

                       2foci: is the points that add up the two distance, which will have the same constant.

                       Eccentricity: measure how much the conic section deviates from being circular.

• foci affects it by giving points that will add up the distance to a constant that id shared by the points.

3.

 

As you can see, this building has the ellipse shape in the center. The creator this building created a living space for someone, that gives a round shape to the house. This modern style creates a relaxing vision toward others eyes.

          Knowing that ellipse are used in the real world, brings excitement towards to math, and real world objects. The real world consists a lot of mathematical equations, and graphs.

 

4. Reference:

http://www.antoninocardillo.com/projects.html

http://www.mathopenref.com/ellipse.html





           

WPP#9: Unit L: Concept 4-8: Fundamental Counting Principles

Create your own Playlist on LessonPaths!

WPP#10 :Unit L Concepts 9-14 : Fundamental Counting Principles

Create your own Playlist on LessonPaths!